Trigonometry Find the Other Trig Values in Quadrant I tan (theta) = square root of 2 tan (θ) = √2 tan ( θ) = 2 Use the definition of tangent to find the known sides of the unit circle right triangle The quadrant determines the sign on each of the values tan(θ) = opposite adjacent tan ( θ) = opposite adjacentIdentities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify Statistics Arithmetic Mean Geometric Mean Quadratic Mean Median Mode Order Minimum Maximum Probability MidRange Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal DistributionProve the Following Trigonometric Identities `Tan^2 Theta Sin^2 Theta Tan^2 Theta Sin^2 Theta` CBSE CBSE (English Medium) Class 10 Question Papers 6 Textbook Solutions Important Solutions 3112 Question Bank Solutions Concept Notes & Videos & Videos 356 Time Tables 12

Proof Tan 2 1 Sec 2 Youtube
Trig identities tan^2 theta
Trig identities tan^2 theta-Tan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos 2 (x) sin 2 (x) = 2 cos 2 (x) 1 = 1 2 sin 2 (x) tan(2x) = 2 tan(x) / (1TRIGONOMETRIC IDENTITIES Reciprocal identities Tangent and cotangent identities Pythagorean identities Sum and difference formulas Doubleangle formulas Halfangle formulas Products as sums Sums as products A N IDENTITY IS AN EQUALITY that is true for any value of the variable (An equation is an equality that is true only for certain values of the variable) In



Tan2x 1 ただの悪魔の画像
1102 Proof of cosine identities;Answer to Verify the trigonometric identity cos^2 theta (1 tan^2 theta) = 1 By signing up, you'll get thousands of stepbystep solutions toFree math lessons and math homework help from basic math to algebra, geometry and beyond Students, teachers, parents, and everyone can find solutions to their math problems instantly
Start studying Trig Identities for Calc 2 test one Learn vocabulary, terms, and more with flashcards, games, and other study toolsTrigonometric functions Here, x is an angle in degrees The sine and cosine functions are periodic with period 360 ∘ The maximum value of these functions is 1 The minimum value is 1 We say that the amplitude is 1 The tangent function is periodic with period 180 ∘The six trigonometric functions are defined for every real number, except, for some of them, for angles that differ from 0 by a multiple of the right angle (90°) Referring to the diagram at the right, the six trigonometric functions of θ are, for angles smaller than the right angle = = = = = = = = = = = = Ratio identities In the case of angles smaller than a right
0 votes 1 answer Prove each of the following identities `(tan theta)/((1 tan^(2) theta)^(2)) (cot theta)/((1 cot^(2) theta)^(2)) = sin theta cos theta ` asked in Trigonometry by Ayush01 (447k points) class10;The key Pythagorean Trigonometric identity are sin 2 (t) cos 2 (t) = 1 tan 2 (t) 1 = sec 2 (t) 1 cot 2 (t) = csc 2 (t) So, from this recipe, we can infer the equations for different capacities additionally Learn more about Pythagoras Trig Identities Dividing through by c 2 gives a 2/ c 2 b 2/ c 2 = c 2/ c 2 This can be simplifiedFor any value of \(x\), this equation is true Trig identities are sort of like puzzles since you have to



Ilectureonline




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
In trigonometry, the secant and tangent are two functions, angle from secant squared of angle is equal to one and it is called as the Pythagorean identity of secant and tangent functions $\sec^2{\theta}\tan^2{\theta} \,=\, 1$ Popular forms The Pythagorean identity of secant and tan functions can also be written popularly in two other forms $\sec^2{x}\tan^2{x} \,=\, 1$ $\sec^2Trigonometry Trigonometric Identities and Equations HalfAngle Identities 1 AnswerTrigonometric identities are equalities involving trigonometric functions An example of a trigonometric identity is sin 2 θ cos 2 θ = 1 \sin^2 \theta \cos^2 \theta = 1 sin2 θcos2 θ = 1 In order to prove trigonometric identities, we generally use other known identities such as Pythagorean identities




Solved Use The Trigonometric Identities To Simplify The Chegg Com




Using Trigonometric Identities Video Khan Academy
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!My issue is understanding the connection between those rules and what exists on the RHS within equation $(1)$ Apologies for any confusion on this25 Proof of Compositions of trig and inverse trig functions;




Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download




Trigonometric Identities Proofs List Of Trig Identities
1tan2θ=sec2θ 1 tan 2 θ = sec 2 θ The second and third identities can be obtained by manipulating the first The identity 1cot2θ = csc2θ 1 cot 2 θ = csc 2 θ is found by rewriting the left side of the equation in terms of sine and cosine Prove 1cot2θ = csc2θ 1 cot 2 θ = csc 2 θThe tan squared function rule is also popularly expressed in two forms in trigonometry $\tan^2{x} \,=\, \sec^2{x}1$ $\tan^2{A} \,=\, \sec^2{A}1$ In this way, you can write the square of tangent function formula in terms of any angle in mathematics Proof Take, the theta is an angle of a right triangle, then the tangent and secant are written as $\tan{\theta}$ and $\sec{\thetaFollowing table gives the double angle identities which can be used while solving the equations You can also have #sin 2theta, cos 2theta# expressed in terms of #tan theta # as under #sin 2theta = (2tan theta) / (1 tan^2 theta)# #cos 2theta = (1 tan^2 theta) / (1 tan^2 theta)#




How To Use Double Angle Identities Studypug



If Tan Theta Cot Theta 2 Then What Is The Value Of Tan Squared Theta Cot Squared Theta Equal To Quora
Prove the Following Trigonometric Identities Cot Theta Tan Theta = (2 Cos^2 Theta 1)/(Sin Theta Cos Theta) CBSE CBSE (English Medium) Class 10 Question Papers 6 Textbook Solutions Important Solutions 3112 Question Bank Solutions Concept Notes &All three of the trigonometric functions of an angle are related If we know the value of one of the three, we can calculate the other two (up to sign) by using the Pythagorean and tangent identities We do not need to find the angle itself in order to do this We need only know in which quadrant the angle lies to determine the correct sign for the trig ratios Example 555 If \(~\sin \thetaCartesian Coordinates Using Cartesian Coordinates we mark a point on a graph by how far along and how far up it is The point (12,5) is 12 units along, and 5 units up Four Quadrants When we include negative values, the x and y axes divide the space up into 4 pieces Quadrants I, II, III and IV (They are numbered in a counterclockwise direction) In Quadrant I both x and y are positive,




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube




32 Prove The Trigonometric Identity Sec 6 Theta Tan 6 Theta 3 Tan 2 Theta Sec 2 Theta If Sec Theta Tan Theta P Find The Value Of Csc Theta
Tan (theta) = 2 this means that opposite divided by adjacent is equal to 2Answers Click here to see ALL problems on Trigonometrybasics Question 4134 tan theta=2 find the five other trigonometric function values Found 2 solutions by Theo, Edwin McCravy Answer by Theo () ( Show Source ) You can put this solution on YOUR website!23 Cosine and angle ratio identity;




Show That The Following Are Not Trigonometric Identities 1 Tan 2x 2tan X 2 Sec X Sqrt 1 Tan 2 X 3 Sin X Y Sin X Sin Y Study Com



Cochranmath Solving Trigonometric Equations
0 votes 1 answer Prove each of the following identities ` (tan theta)/((1cot theta)) (cot theta)/((1 tanUsing trigonometric identities Trigonometric identities like sin²θcos²θ=1 can be used to rewrite expressions in a different, more convenient way For example, (1sin²θ) (cos²θ) can be rewritten as (cos²θ) (cos²θ), and then as cos⁴θ Created by Sal Khan This is What is #tan(theta/2)# in terms of trigonometric functions of a unit #theta#?




Understanding Pythagorean Identities Studypug



Solved Consider The Possible Identity Tan 2x Cos 2x 1 Cos 2x Sec 2x A State Any Non Permissible Values B Attempt To Verify Possible Identity Course Hero
2 Identities involving calculus 21 Preliminaries; Trigonometric Identities Basic Definitions Definition of tangent $ \tan \theta = \frac{\sin \theta}{\cos\theta} $ Definition of cotangent $ \cot \theta = \frac{\cos Use trigonometric identities to transform the left side of the equation into the right side \(\displaystyle \tan{\theta} \cot{\theta}={1}\)
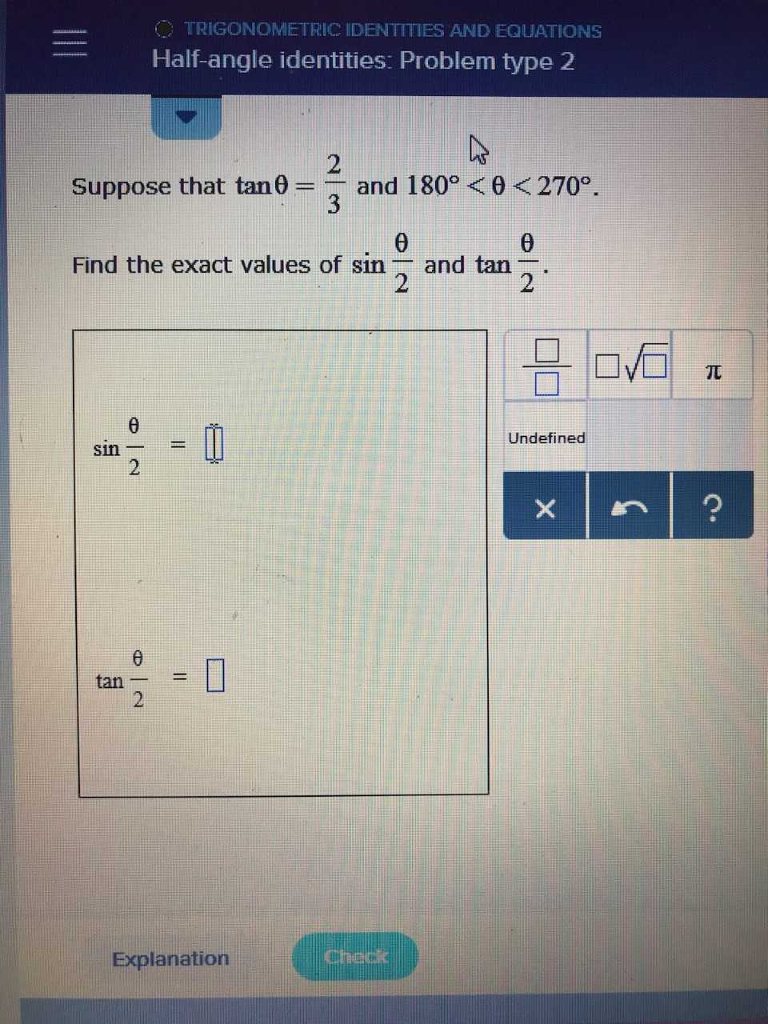



Solved Trigonometric Identities And Equations Half Angle Chegg Com




How Do You Simplify Sec 4x Tan 4x Sec 2x Tan 2x Socratic
1101 Proof of sine identities; Half Angle Formula Cosine Using a similar process, with the same substitution of `theta=alpha/2` (so 2θ = α) we subsitute into the identity cos 2θ = 2cos 2 θ − 1 (see cosine of a double angle) We obtain `cos alpha=2\ cos^2(alpha/2)1`All the trigonometric identities on one page Color coded Mobile friendly With PDF and JPG downloads Trig Identities Download PDF Download JPG Reciprocal Identities I highly recommend this 3minute



What Should I Study To Know How To Solve Example



3
Like looking in a mirror An example of a trig identity is \(\displaystyle \csc (x)=\frac{1}{\sin (x)}\);Visit http//ilectureonlinecom for more math and science lectures!In this video I will solve tan^2(theta)4=0, theta=?This animation, created using MATLAB, illustrates why using the trig substitution x = a tan(theta) can be helpful in evaluating an integral containing the ra




Solved Following Are A List Of Trigonometric Identities Chegg Com
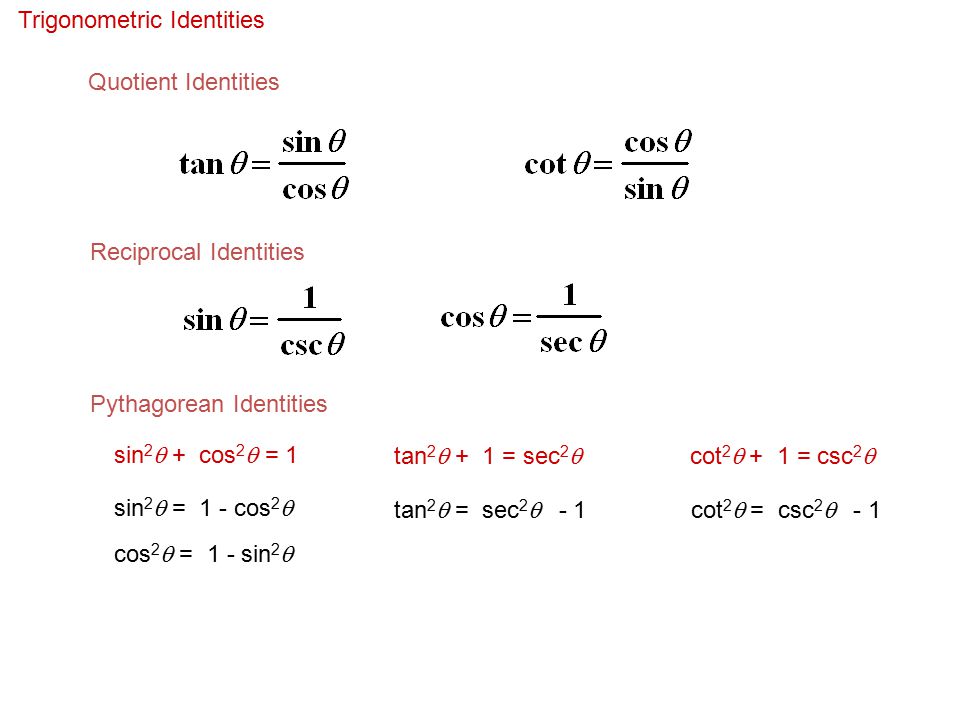



11 Basic Trigonometric Identities An Identity Is An Equation That Is True For All Defined Values Of A Variable We Are Going To Use The Identities To Ppt Download
It is a method for finding antiderivatives of functions which contain square roots of quadratic expressions or rational powers of the form n 2 (where n is an integer) of quadratic expressions Examples of such expressions are 4 − x 2 a n d ( x 2 1) 3 / 2 The method of trig substitution may be called upon when other more common and easierTrig Identities In this problem we want to use one of the fundamental trig identities to write the given expression as an integer Since we have secant and tangent functions62 Trigonometric identities (EMBHH) An identity is a mathematical statement that equates one quantity with another Trigonometric identities allow us to simplify a given expression so that it contains sine and cosine ratios only This enables us to solve equations and also to prove other identities Quotient identity




Worksheet On Trigonometric Identities Establishing Identities Hints
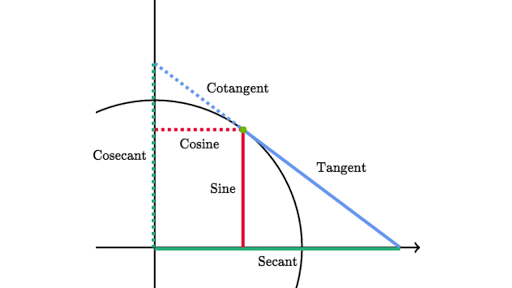



Trig Identity Reference Article Khan Academy
Trig identities stuck solving $\tan^2\theta = \frac 32 \sec\theta$ Ask Question Asked 4 years, 4 months ago Active 4 years, 4 months ago Viewed 156 times 2 0 $\begingroup$ Solve the equation on the interval $0\leq \theta < 2\pi$ $$\tan^2 \theta = \frac{3}{2}\sec \theta $$ Here are the steps I have so far Identity $\tan^2 \theta = \sec^2 \theta 1 $ Substitute $$\sec^2 \theta 124 Cosine and square of angle ratio identity;An "identity" is something that is always true, so you are typically either substituting or trying to get two sides of an equation to equal each otherThink of it as a reflection;




Summary Of Trigonometric Identities



Tan2x 1 ただの悪魔の画像
For the sake of clarification, I'm also aware of the double angle rules and how they are used to obtain $\tan^2(\frac{\theta}{2})$;Trigonometric Identities Solver \square!Trig identities tan^2Section 71 Solving Trigonometric Equations and Identities 413 Try it Now 2 Solve 2 2sin ( ) 3cos(t t ) for all solutions t 0 2 In addition to the Pythagorean identity, it is often necessary to rewrite the tangent, secant,Periodicity of trig functions Sine, cosine, secant, and cosecant have period 2 π while tangent and cotangent have period π Identities for negative




Solved Establish The Identity 1 Tan 2 Theta 1 Tan 2 Chegg Com




Integrate Tan 2x
We have certain trigonometric identities Like sin 2 θ cos 2 θ = 1 and 1 tan 2 θ = sec 2 θ etc Such identities are identities in the sense that they hold for all value of the angles which satisfy the given condition among them and they are called conditional identities Trigonometric Identities With Examples Example 1 Prove the following trigonometric identities (i) (1 – sin 2Differentiation of Trigonometric Functions It is possible to find the derivative of trigonometric functions Here is a list of the derivatives that you need to know d (sin x) = cos x dx d (cos x) = –sin x dx d (sec x) = sec x tan x dx22 Sine and angle ratio identity;
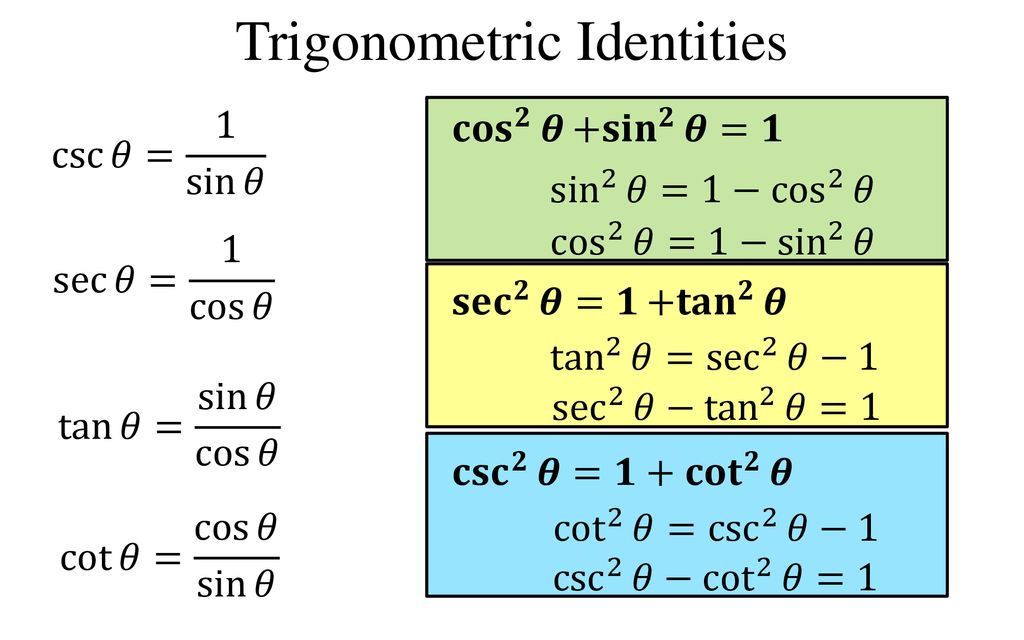



Trigonometric Identities And Equations Ppt Download



Much From Little




How To Solve Tan 2xsin 2x Tan 2x Sin 2x Trigonometry Trigonometric Identities Youtube




How Do You Prove Tan 2x Secx 1 1 Secx Socratic




Trigonometric Identities Sin 2 X Cos 2 X Tan 2 X Youtube
x-1=sec(squared)x.jpg)



10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com




Cos 2x Formula Derivation Examples What Is Cos 2a Formula




Integrate Sec 2x Method 2




Proof Tan 2 1 Sec 2 Youtube




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic




How Do You Use The Fundamental Trigonometric Identities To Determine The Simplified Form Of The Expression Socratic



Complex And Trigonometric Identities Introduction To Digital Filters



Bestmaths Online Proof 4




Tangent Half Angle Formula Wikipedia




Solved 2 Prove The Following Trig Identities A Prove Tan Chegg Com




What Is The Integration Of Tan 2x Solution Quora




Trigonometric Identities With Pdf Download Math Tutor




Analytic Trig Ppt Video Online Download




Trigonometric Identities Sin 2 X Cos 2 X Tan 2 X Notes Hive




5 1 Fundamental Trig Identities Reciprocal Identities Sin




5 1 Fundamental Trig Identities Reciprocal Identities Sin




Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube




How Do You Verify The Identity Tan2theta 2 Cottheta Tantheta Socratic
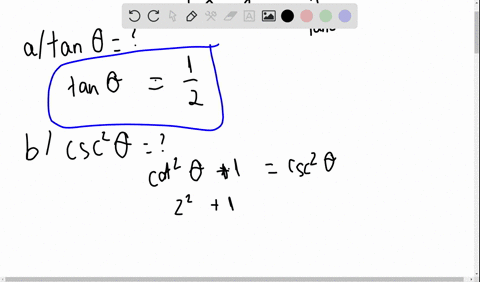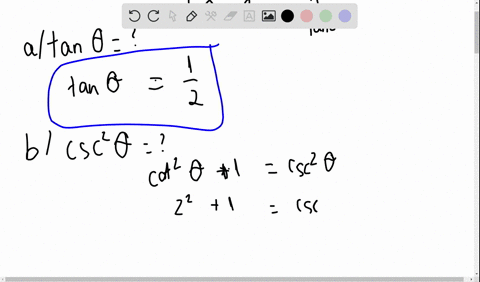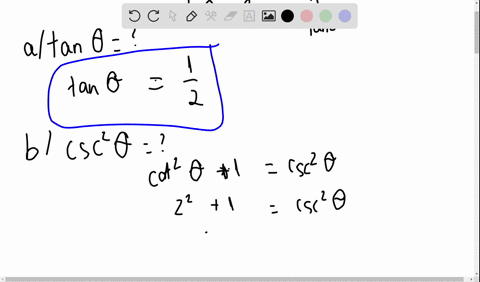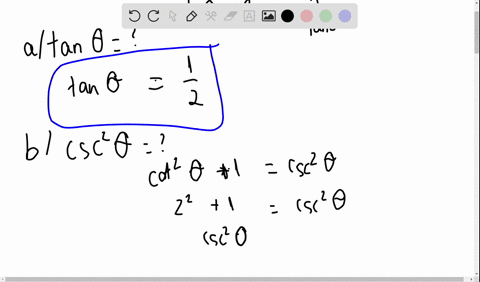



Solved Given Tan Theta 4 Use Trigonometric Identities To Find The Exact Value Of A Sec 2 Theta B Cot Theta C Cot Left Frac Pi 2 Theta Right D Csc 2 Theta
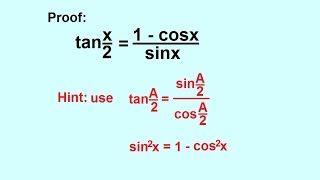



Precalculus Trigonometry Trig Identities 34 Of 57 Proof Half Angle Formula Tan X 2 Youtube



Trigonometry Identities




14 2 Trigonometric Identities



Important Trigonometric Identiti




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic



Solving Trigonometric Equations With Identities Precalculus Ii




List Of The Basic Trig Identities Video Lesson Transcript Study Com




Trigonometric Identities




The Reciprocal Trigonometric Functions Problem 3 Trigonometry Video By Brightstorm



1




Trigonometry Reciprocal Identities Expii
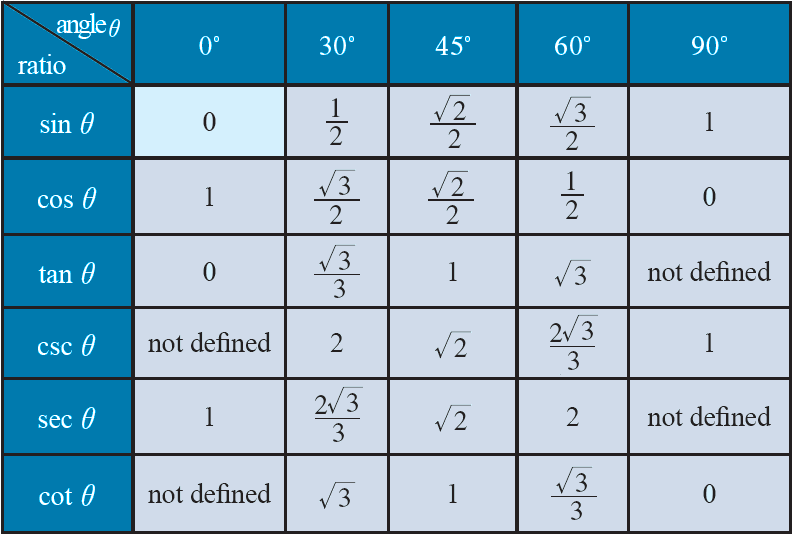



Trigonometric Identities



Solving Trigonometric Equations With Identities Algebra And Trigonometry



How I Remember Trig Identities Part 2 Beyond Solutions




Tangent Half Angle Formula Wikipedia



The Trigonometric Ratios Of Angl




上 Tan2x Identity ただの悪魔の画像




Summary Of Trigonometric Identities
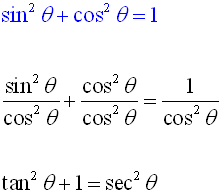



Pythagorean Identities Mathbitsnotebook Ccss Math




How Does The Trigonometric Identity 1 Cot 2 Theta Csc 2 Theta Derive From The Identity Sin 2 Theta Cos 2 Theta 1 Mathematics Stack Exchange




Trigonometric Identities List Of Trigonometric Identities Examples



1



What Is The Formula Of Tan2x Quora



Ilectureonline




Solving Trigonometric Equations And Inequalities Precalculus




4 1 Revision Trigonometry Siyavula




List Of Trigonometric Identities Wikipedia
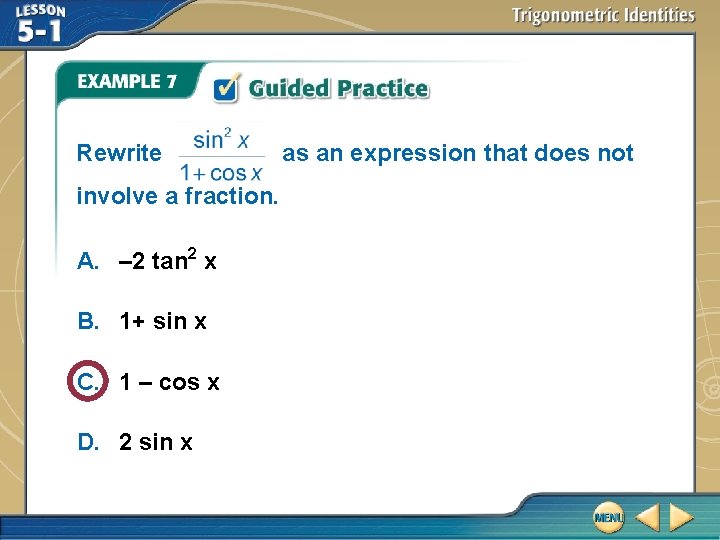



Lesson 5 1 Trigonometric Identities Fiveminute Check Over




Trigonometric Identities A Plus Topper
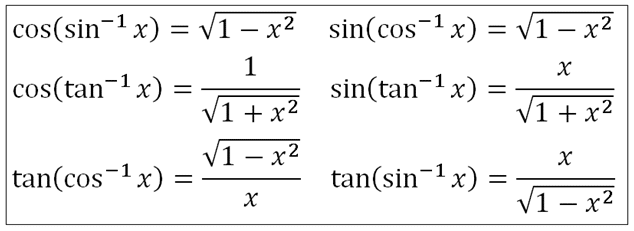



Inverse Trig Identities Reciprocal Of Trigonometric Function Trig




Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions




Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download



Pythagorean




How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic




bestpictjcry Tan 2x Tan 2x
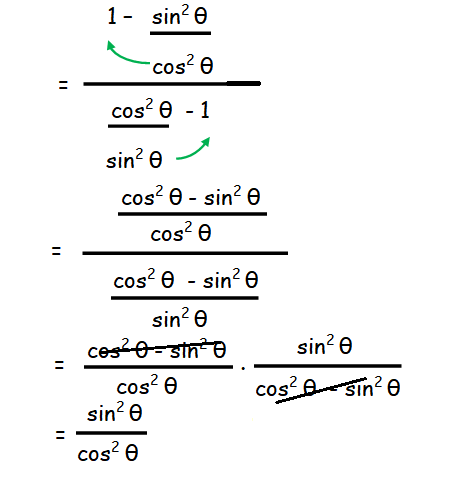



Proving Trigonometric Identities




How Do You Verify 4tan 4 Tan 2x 3 Sec 2x 4tan 2x 3 Kinda Hard Please With All The Steps Thanks Socratic



Which Of The Following Is A Trigonometric Identity A Cot Theta Tan Theta 1b Brainly Com




Trigonometric Identities Topics In Trigonometry




How Does The Trigonometric Identity 1 Cot 2 Theta Csc 2 Theta Derive From The Identity Sin 2 Theta Cos 2 Theta 1 Mathematics Stack Exchange
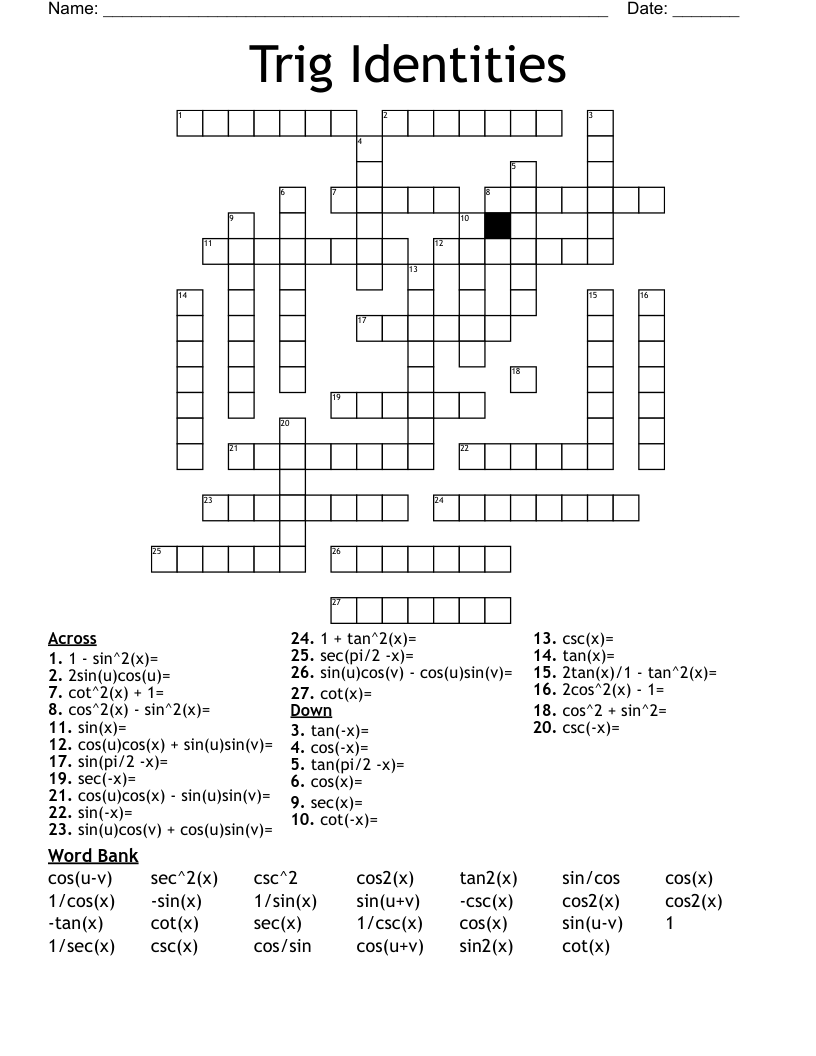



Trig Identities Crossword Wordmint



2




Trigonometric Identities A Plus Topper




5 1 5 2 Trigonometric Identities Ppt Download



Trigonometry Identities




Art Of Problem Solving



How Do You Verify Tan 28 Sin 28 Tan 28sin 28 Socratic
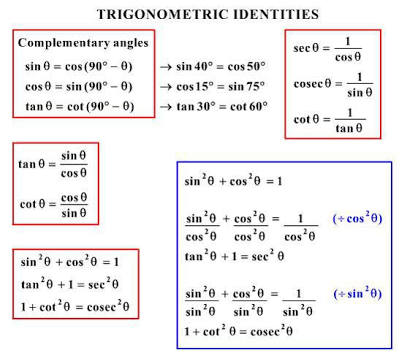



How Do You Simplify The Expression Sin 2theta Cos 2theta Cos 2theta Socratic



Relating Trigonometric Functions Trigonometry Socratic




Double Angle Identities Trigonometry Socratic




Solved Does Tan 2 Theta Frac Sin 2 Theta Cos 2 Theta Justify Your Answer




Integrate Cosec 2x




Summary Of Trigonometric Identities



Trigonometric Identities



0 件のコメント:
コメントを投稿